빠똥빠똥
17298번 오큰수(stack) - ☆ 본문
#문제링크 : www.acmicpc.net/problem/17298
<전략>
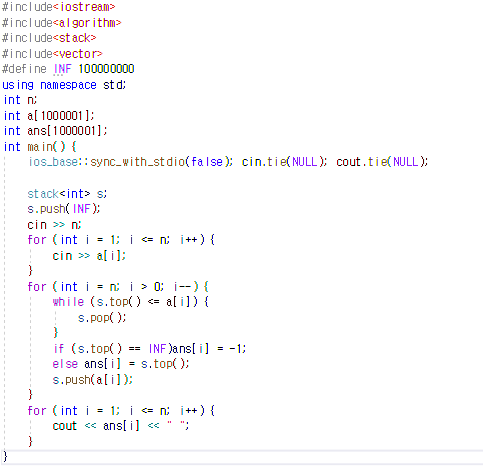
1. O(N^2)의 알고리즘 밖에 떠오르지 않아서 다른 블로그를 참조했습니다.
2. 개인적으로 생각하기 굉장히 어려운 알고리즘이었습니다. 요약하면 이렇습니다. 우선 스택을 만들고, 스택에, 문제에서 주어진 수의 범위보다 큰 수를 미리 하나 넣어놓습니다. 그리고 주어진 수열의 뒤에서부터 차례로 스택top의 숫자와 비교합니다.
3. 만약, 수열의 숫자가 스택top보다 작다면, 스택top에 들어있는 숫자가 오큰수가 됩니다. 따라서, 이때에는 스택top의 숫자를 해당 수열의 인덱스와 같은 정답 배열에 우선 복사하고, 수열 숫자를 스택에 push합니다. (이 과정에서 pop은 없습니다.)
4. 만약, 수열의 숫자가 스택top보다 크다면, 스택top에 들어있는 숫자는 오큰수가 아닙니다. 따라서, 수열의 숫자보다 큰 수가 나올때까지, 스택을 pop합니다. 맨 처음에, 주어진 범위의 수보다 큰 수를 담아놨기 때문에, 오큰수가 없는 경우여도 무조건 스택empty가 되기 전에 pop이 멈추게 됩니다.
5. 4에서 pop을 하고 멈췄을 때, 그때의 스택top이 오큰수 이므로 3의 과정을 반복하면 됩니다. 만약, 처음 담아두었던 값이 스택top이라면 3의 과정에서 복사하는 숫자를 -1로 해주면 됩니다.
6. 예를 들어보겠습니다.
INF=1억 이라 하면, stack s에 s.push(INF) 해놓습니다.
A = < 9 5 3 2 4 7 6 > ANSWER = < 0 0 0 0 0 0 0 >
S = INF
INF > 6 이므로, ANSWER배열에 6이 있던 위치에 -1을 넣고, 스택에 6을 추가합니다.
A = < 9 5 3 2 4 7 6 > ANSWER = < 0 0 0 0 0 0 -1 >
S = INF 6
6 < 7 이므로, 스택에서 7보다 큰 수가 top이 될때까지 pop합니다.
A = < 9 5 3 2 4 7 6 > ANSWER = < 0 0 0 0 0 0 -1 >
S = INF
INF > 7 이므로, ANSWER배열에 7이 있던 위치에 -1을 넣고, 스택에 7을 추가합니다.
A = < 9 5 3 2 4 7 6 > ANSWER = < 0 0 0 0 0 -1 -1 >
S = INF 7
7 > 4 이므로, ANSWER배열에 4가 있던 위치에 7을 넣고, 스택에 4를 추가합니다.
A = < 9 5 3 2 4 7 6 > ANSWER = < 0 0 0 0 7 -1 -1 >
S = INF 7 4
4 > 2 이므로, ANSWER배열에 2가 있던 위치에 4을 넣고, 스택에 2를 추가합니다.
A = < 9 5 3 2 4 7 6 > ANSWER = < 0 0 0 4 7 -1 -1 >
S = INF 7 4 2
2 < 3 이므로, 스택에서 3보다 큰 수가 top이 될때까지 pop합니다.
A = < 9 5 3 2 4 7 6 > ANSWER = < 0 0 0 4 7 -1 -1 >
S = INF 7 4
4 > 3 이므로, ANSWER배열에 3가 있던 위치에 4을 넣고, 스택에 3를 추가합니다.
A = < 9 5 3 2 4 7 6 > ANSWER = < 0 0 4 4 7 -1 -1 >
S = INF 7 4 3
3 < 5 이므로, 스택에서 5보다 큰 수가 top이 될때까지 pop합니다.
A = < 9 5 3 2 4 7 6 > ANSWER = < 0 0 4 4 7 -1 -1 >
S = INF 7
7 > 5 이므로, ANSWER배열에 5가 있던 위치에 7을 넣고, 스택에 5를 추가합니다.
A = < 9 5 3 2 4 7 6 > ANSWER = < 0 7 4 4 7 -1 -1 >
S = INF 7 5
5 < 9 이므로, 스택에서 9보다 큰 수가 top이 될때까지 pop합니다.
A = < 9 5 3 2 4 7 6 > ANSWER = < 0 7 4 4 7 -1 -1 >
S = INF
INF > 9 이므로, ANSWER배열에 9가 있던 위치에 -1을 넣고, 스택에 9를 추가합니다.
A = < 9 5 3 2 4 7 6 > ANSWER = < -1 7 4 4 7 -1 -1 >
S = INF 9
7. 정확한 시간복잡도는 모르겠지만, 수열의 뒷부분부터 앞쪽까지 전체 수열을 검토할 동안, 스택에 지나쳐온 수열값들을 그대로 담으므로 O(N) 정도가 아닐까 생각됩니다. 최대의 경우인 100만개의 원소를 갖는 수열이라 했을 때, 모든 원소들이 스택에 한번씩 push되고, 수열비교도 한번씩 되므로 "수열 비교하는 경우 + 스택에 push/pop"이라 할 수 있습니다. "뒤에서부터 앞까지 비교하는 데 100만 + 스택push가 100만 + 오큰수가 아닌 수 pop 100만 이하" 로 N의 상수배정도로 생각할 수 있을 것 같습니다.
'백준' 카테고리의 다른 글
| 1916번 최소비용 구하기(다익스트라) - ☆ (0) | 2021.03.13 |
|---|---|
| 11444번 피보나치 수6 (행렬거듭제곱) (0) | 2021.01.19 |
| 13305번 주유소(그리디) - ☆ (0) | 2021.01.18 |
| 9184번 신나는 함수 실행(DP, 재귀) (0) | 2021.01.18 |
| 1655번 가운데를 말해요(우선순위 큐) - ☆ (0) | 2020.09.08 |




